Сферические купола из полос бумаги представляют собой необычную модель в плане исполнения, и очень хрупкую при транспортировке и демонстрации. Работа с учащимися на внеклассных занятиях по данной теме требует изображения икосододекаэдра, т.е. чертежа.
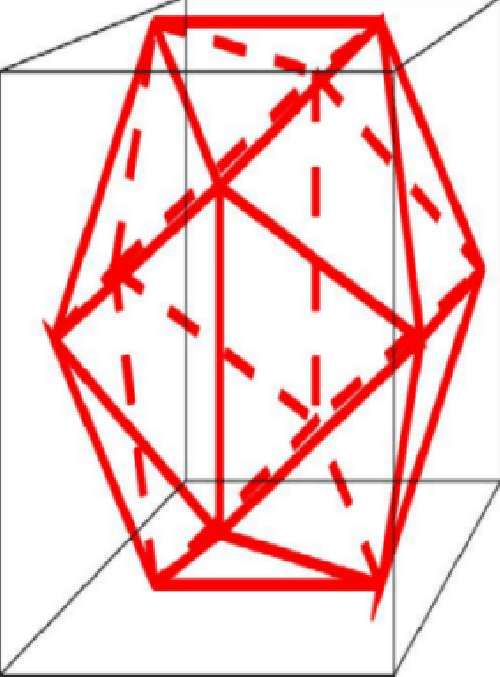
Предположим, что икосаэдр вписан в куб; так как противоположные ребра икосаэдра параллельны, скрещивающиеся ребра взаимно перпендикулярны, у икосаэдра 12 вершин, то на каждой грани куба расположено по две вершины икосаэдра. Из соображений симметрии они будут лежать на средних линиях граней куба.
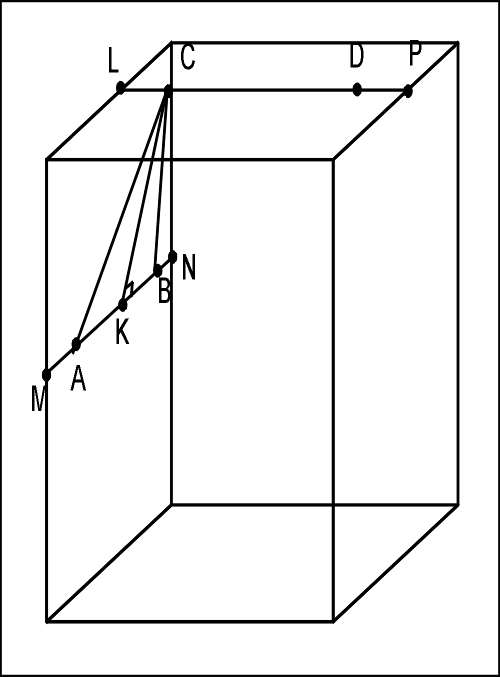
Пусть A, B, C, D —вершины икосаэдра; ребро куба равно 1, ребро икосаэдра равно x.Обозначим: LC=y, тогда 1=x+2y, где 1 - ребро куба. Рассмотрим CLK:CL=y, LK =1/2, тогда CK*CK= y*y +(1/4) . Рассмотрим треугольник ABC — это грань икосаэдра: CK —высота, тогда CK*CK=3*x*x*2/4.
Получим систему
x+2*y=1 4y*y - 3x*x =-1Решив систему, получим два значения: y1=(3+v5)/4 и y2=(3 - v5)/4. Но y1›1, т.е. больше стороны куба; y2=0.2 — есть искомое решение.Итак y=(3-v5)/4,это —формула конструктивная, т.е. все вершины и сам икосаэдр построить можно.